Comparison

The evaluable predicates described in this section are meta-logical. They are used to compare and order terms, rather than to evaluate or process them. They treat uninstantiated variables as objects with values which may be compared, and they never instantiate those variables. Each of these predicates simply succeeds or fails; there is no side-effect, substitution or error condition associated with them. The predicates described in this section should not be used when what the user really wants is arithmetic comparison predicates or unification predicates (see section 6.3).

The predicates described take into account a standard total ordering of terms, which has as follows:

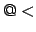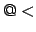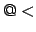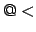variables $$\tt @<$$ floating point numbers $$\tt @<$$ integers $$\tt @<$$ atoms $$\tt @<$$ compound terms

Within each one of the categories, the ordering is as follows:

• variables are put in a standard order (roughly, the oldest first -- the order is not related to the names of variables). Also, note that two anonymous variables are not identical terms. Unfortunately in the current implementation of our system (Version 2.5) variables ``tend to move'' rather quickly as a result of unification, and thus the ordering may not continue to hold if the variables get unified to some other variables. We intend to ameliorate this bug in future releases.
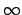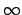• floating point numbers and integers are put in numeric order, from - $\infty$ to + $\infty$. Note that a floating point number is always less than an integer, regardless of their numerical values.
• atoms are put in alphabetical (i.e. ASCII) order;
• compound terms are ordered first by arity, then by the name of their principal functor and then by their arguments (in a left-to-right order).
• lists are compared as ordinary compound terms having arity 2 and functor '.'.

For example, here is a list of terms sorted in increasing standard order:

[ X, 3.14, -9, fie, foe, fum(X), [X], X = Y, fie(0,2), fie(1,1) ]

The basic predicates for comparison of arbitrary terms are:

T1 == T2

Tests if the terms currently instantiating T1 and T2 are literally identical (in particular, variables in equivalent positions in the two terms must be identical). For example, the question:

| ?- X == Y.

fails (answers no) because X and Y are distinct variables. However, the question

| ?- X = Y, X == Y.

succeeds because the first goal unifies the two variables (see section 6.3).

Tests if the terms currently instantiating T1 and T2 are not literally identical.

T1 @< T2

Succeeds if term T1 is before term T2 in the standard order.

T1 @> T2

Succeeds if term T1 is after term T2 in the standard order.

T1 @= < T2

Succeeds if term T1 is not after term T2 in the standard order.

T1 @> = T2

Succeeds if term T1 is not before term T2 in the standard order.

Some further predicates involving comparison of terms are:

compare(?Op, +T1, +T2)

Succeeds if the result of comparing terms T1 and T2 is Op, where the possible values for Op are:

`='

if T1 is identical to T2,

`<'

if T1 is before T2 in the standard order,

`>'

if T1 is after T2 in the standard order.

Thus compare(=, T1, T2) is equivalent to T1==T2. Predicate compare/3 has no associated error conditions.

sort(+L1, ?L2)

The elements of the list L1 are sorted into the standard order, and any identical (i.e. `==') elements are merged, yielding the list L2. The time to perform the sorting is O(nlogn) where n is the length of list L1.

Examples:

                | ?- sort([3.14,X,a(X),a,2,a,X,a], L).

                L = [X,3.14,2,a,a(X)];

                no

Exceptions:

instantiation_error

Argument 1 of sort/2 is a variable or is not a proper list.

keysort(+L1, ?L2)

The list L1 must consist of elements of the form Key-Value. These elements are sorted into order according to the value of Key, yielding the list L2. The elements of list L1 are scanned from left to right. Unlike sort/2, in keysort/2 no merging of multiple occurring elements takes place. The time to perform the sorting is O(nlogn) where n is the length of list L1. Note that the elements of L1 are sorted only according to the value of Key, not according to the value of Value. The sorting of elements in L1 is not guaranteed to be stable.

Examples:

                | ?- keysort([3-a,1-b,2-c,1-a,3-a], L).

                L = [1-b,1-a,2-c,3-a,3-a];

                no

Exceptions:

instantiation_error

Argument 1 of keysort/2 is a variable or is not a proper list.

type_error

The elements of L1 are not of the form Key-Value.